近几年许多省市中考题中,常出现带系数的两线段和的最值问题,这类问题基本都要用到“阿氏圆”(文章已发布)和“胡不归”模型。本文讲解“胡不归模型”的应用。
【问题源头】
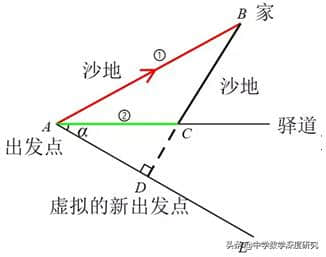
从前,有一个小伙子在外地当学徒,当他获悉在家的老父亲病危的消息后,便立即启程赶路。由于思乡心切,他只考虑了两点之间线段最短的原理,所以选择了全是沙地的直线路径A→B(如图所示),而忽视了走折线,虽然路程多但速度快的实际情况,当他气喘吁吁地赶到家时,老人刚刚咽了气,小伙子失声痛哭。邻居劝慰小伙子时告诉说,老人弥留之际不断念叨着"胡不归?胡不归?…"。这个古老的传说,引起了人们的思索,小伙子能否提前到家?倘若可以,他应该选择一条怎样的路线呢?这就是风靡千百年的"胡不归问题"。

【数学处理】
我们把这个问题简化为数学模型,假设在沙地上的速度是v,在驿道上的速度是u,且v:u=k(k<1)。由于我们比较的是时间的长短,路线①很容易计算,但是路线②因为两段路程的速度不同很难计算。数学上总是喜欢把没见过的问题转化为已知的问题,如果能让路线②的两段速度一样就好办了!可是如果让路线②在驿道上的速度慢下来,时间就变长了,为了保证时间不变,我们需要通过特殊方法缩短路线②的路程。

【模型建立】
在AC下方取一条射线AE,过点C作AE的垂线交于点D,使得CD:AC=k,我们发现,只要使得射线AC与AE的夹角的正弦值等于k,就能让CD:AC=k永远成立。
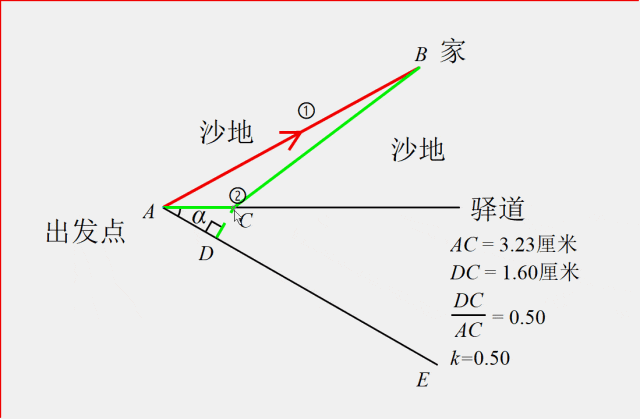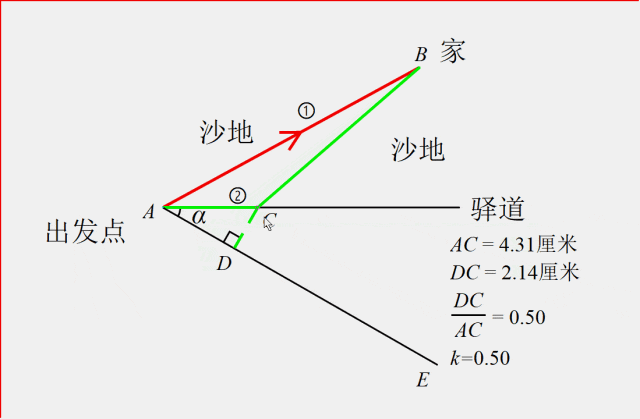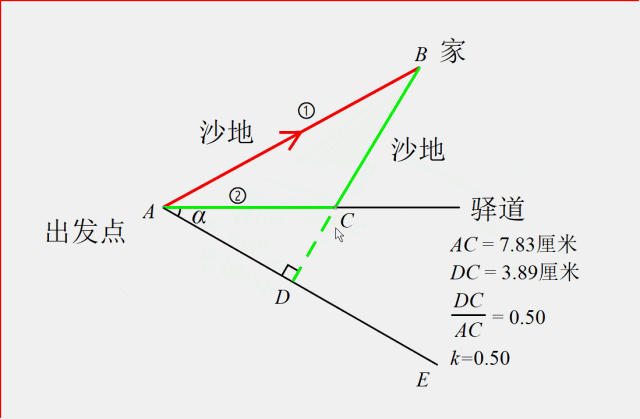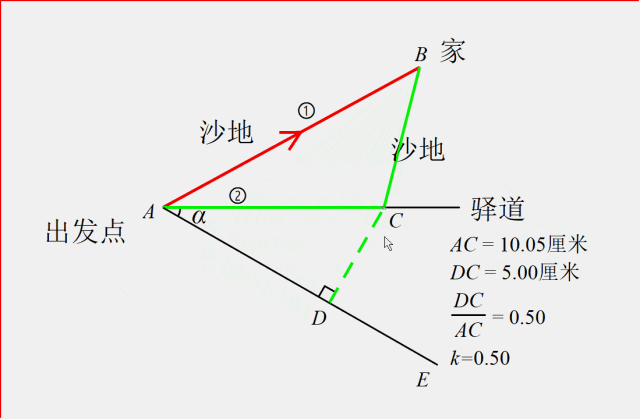
这样正好使得高速度u在A-C上花的时间等于低速度v在D-C上花的时间。
【构图的意义】
原本路线②是从A-C-B,其中A-C路线速度为u,C-B路线速度为v,现在路线②是从D-C-B,全程速度为v,且时间不变 且无论C点在什么位置,由于AE是定直线,这个比值关系是一直成立的。 那么我们就把变速问题转化为了匀速问题;现在新的出发点是点D,路线为D-C-B,全程速度为v!
那么,点C选在哪的时候,路程最短呢? 这个答案是显而易见的,由于速度不变,时间最短时路程最短, 因为点B和直线AE都是固定的,所以最短距离就是点B到直线AE所做的垂线段。
这个方案是最快的,不仅比路线①快(直角三角形斜边大于直角边),而且比路线②的其它C点的位置的情况都要快。

角度很方便就能计算出来,这样去画图,看来操作性不错!
我们已经解决了古人回家的问题,那么这个思想怎么运用在数学题目当中呢?

【数学题中的运用】
加权线段和kPA+PB(k<1)的最小值问题:
如图,点P是直线上的一个动点,点A在直线上,点B在直线外,找到加权线段和kPA+PB(k<1)最小时点P的位置。(其中假设k=0.4)
通过动态图,我们发现确实存在一个点P,使得这个值最小.那么要如何找到这个点的位置呢?
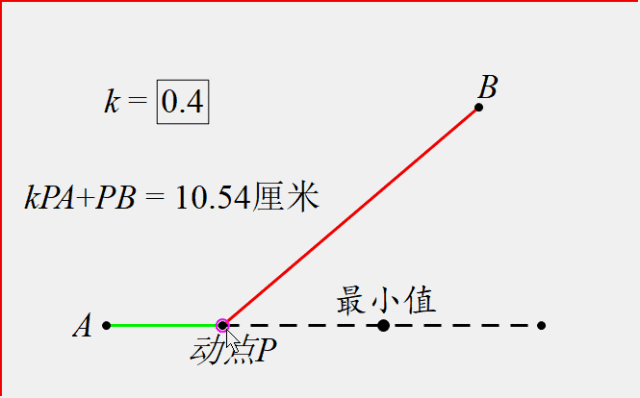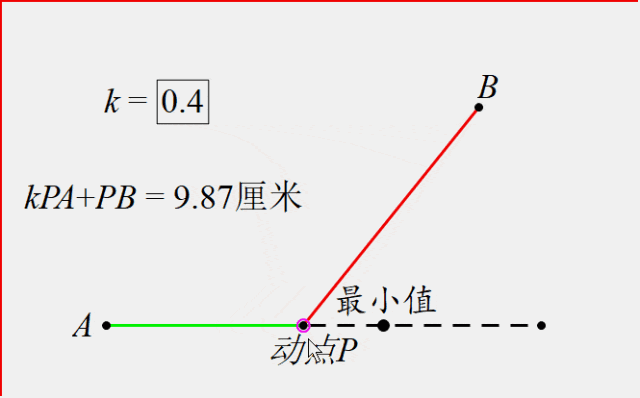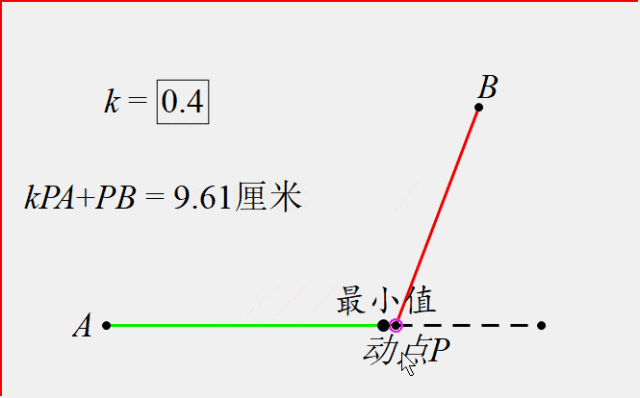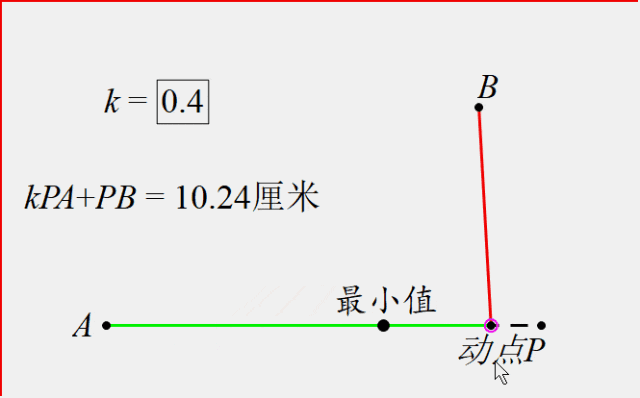
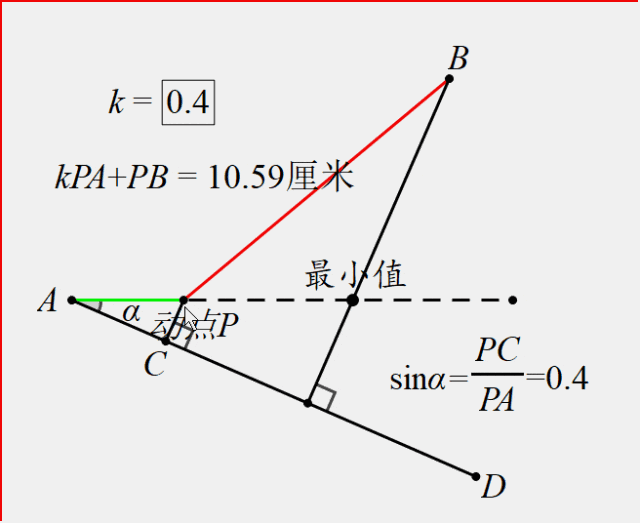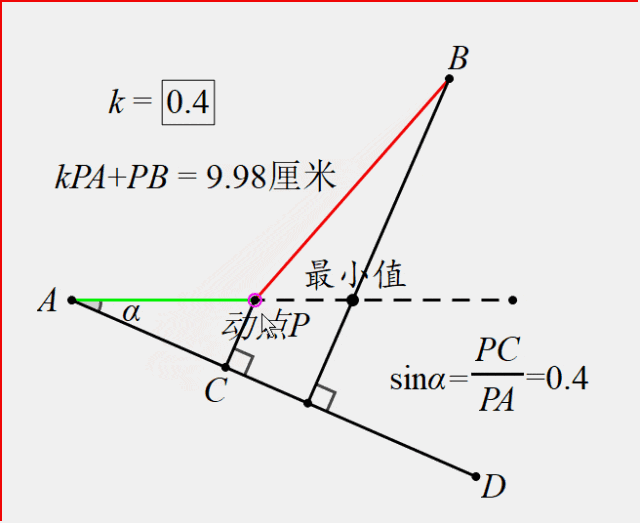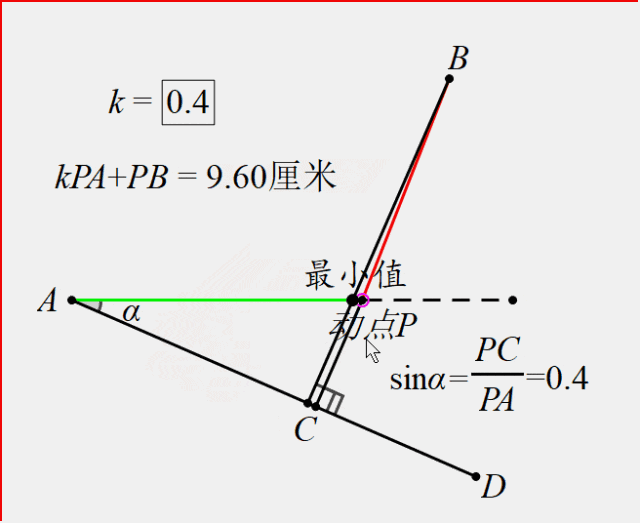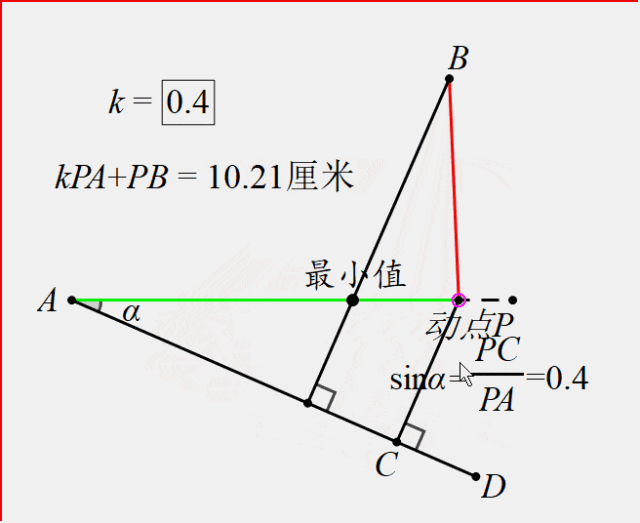
方法:构造射线AD,使得sin∠DAP=k(此例k=0.4),过点P作AD垂线段PC,于是PC=kPA,所以kPA+PB的最值问题就转化为PC+PB的问题,过点B作垂线段就能就解决问题。
这时,有同学会问,如果是2a+3b问题怎么办?其实这都是出题人耍的花招,转化为3(2/3a+b)就行了不是吗?
【拓展延伸】
偷偷告诉你,胡不归问题在自然界中的非常常见,比如光在遇到这类问题的时候也会选择最短时间的路线去走(光的折射斯涅耳定律:光的折射定律(斯涅尔定律):光入射到不同介质的界面上会发生反射和折射。其中入射光和折射光位于同一个平面上,并且与界面法线的夹角满足如下关系: n1sinθ1 = n2sinθ2 其中,n1和n2分别是两个介质的折射率,θ1和θ2分别是入射光(或折射光)与界面法线的夹角,叫做入射角和折射角。 以上公式又叫斯涅尔公式)胡不归问题可以看成是入射角为90°的光的折射问题。

这么具有丰富内涵的模型,新修订的课程标准涉及初高中的内容 "数学学科核心素养",明确提出将"数学文化"融入课程内容,近年来年来中考数学为了体现考查数学文化,很多考题中蕴含这一模型的影子,我们再来看看下面几道问题吧
例1.一条笔直的公路l穿过草原,公路边有一卫生站A,距公路30km的地方有一居民点B,A,B之间的距离为90km.一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是60km/h,在草地上行驶的最快速度是30km/h.问司机应以怎样的路线行驶,所用的行车时间最短?最短时间是多少?
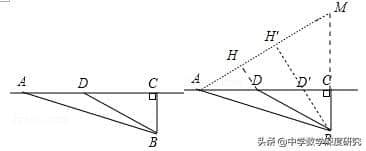
【分析】要求所用行车时间最短,就要计算好行驶的路线,可以设在公路上行驶x,根据题意,找出可以运用勾股定理的直角三角形,运用勾股定理求解.
【解答】解法:1:作射线AM交BC的延长线于M,使得∠MAC=30°,作DH⊥AM.∵时间t=AD/60+BD/30=1/30(1/2AD+BD),DH=1/2AD,
∴时间t=1/30(DH+BD),
∴当D,H,B共线,且BH⊥AM时,时间t最小,
作BH′⊥AM于H′交AC于D′,此时时间最小值=1/30•BH′,
∵AB=90,BC=30,∴AC=60√2,∴CM=AC•tan30°=20√6,
在Rt△BMH′中,BH′=BM•cos30°=(20√6+30)×√3/2=30√2+15√3,
∴t的最小值=√2+√3/2.此时AD′=60√2-10√3.

【点评】本题考查的是在直角三角形中勾股定理的运用,画出图形构建直角三角形是关键,没有比较就没有伤害,两种解法:一种几何法,一种代数法,繁简不同,你可哪一种容易掌握呢?

例2.如图,△ABC在直角坐标系中,AB=AC,A(0,2√2),C(1,0),D为射线AO上一点,一动点P从A出发,运动路径为A→D→C,点P在AD上的运动速度是在CD上的3倍,要使整个运动时间最少,则点D的坐标应为( )
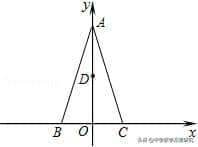
A.(0,√2) B.(0,√2/2)
C.(0,√2/3) D.(0,√2/4)
【分析】假设P在AD的速度为3,在CD的速度为1,首先表示出总的时间,再根据根的判别式求出t的取值范围,进而求出D的坐标.
【解答】解法一:假设P在AD的速度为3V,在CD的速度为1V,

解法二:假设P在AD的速度为3,在CD的速度为1,


例3(2018•无锡中考)如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是_______.
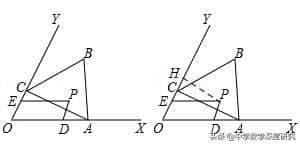
【分析】作辅助线,构建30度的直角三角形,先证明四边形EODP是平行四边形,得EP=OD=a,在Rt△HEP中,∠EPH=30°,可得EH的长,计算a+2b=2OH,确认OH最大和最小值的位置,可得结论.
【解答】过P作PH⊥OY交于点H,
∵PD∥OY,PE∥OX,∴四边形EODP是平行四边形,∠HEP=∠XOY=60°,
∴EP=OD=a,Rt△HEP中,∠EPH=30°,∴EH=1/2EP=1/2a,
∴a+2b=2(1/2a+b)=2(EH+EO)=2OH,
当P在AC边上时,H与C重合,此时OH的最小值=OC=1/2OA=1,即a+2b的最小值是2;当P在点B时,OH的最大值是:1+1/2=5/2,即(a+2b)的最大值是5,∴2≤a+2b≤5.
【点评】本题考查了等边三角形的性质、直角三角形30度角的性质、平行四边形的判定和性质,有难度,掌握确认a+2b的最值就是确认OH最值的范围.

例4(2018•连云港模拟)如图,P为正方形ABCD对角线BD上一动点,若AB=2,则AP+BP+CP的最小值为( )
A.√2+√5 B.√2+√6
C.4 D.3√2
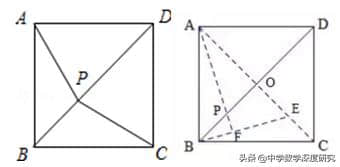
解析:∵正方形ABCD为轴对称图形,∴AP=PC,
∴AP+BP+CP=2AP+BP=2(AP+1/2BP), ∴即求AP+1/2BP的最小值。
这需要我们构造一个1/2 BP出来,连接AE, 作∠DBE=30°,角AC于E,过A作AF⊥BE,垂足为F, 在Rt△PBF中,∵∠PBF=30°,∴PF=1/2BP.由此我们把1/2BP构造出来了,∴AP+1/2BP的最小值即为AF的长。∵∠BAE=45°,
∠AEB=60°,∴解直角三角形△ABE,得AO=BO=√2,OE=√6/3,OB=2√6/3,
根据面积法:1/2AE·BO=1/2BE·AF,可求出AF=√2+√6,故选B.

例5.如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
(1)证明:CE是⊙O的切线;
(2)设点D是线段AC上任意一点(不含端点),连接OD,当AB=8时,求1/2CD+OD的最小值.
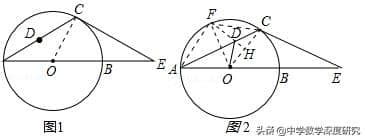
【分析】(1)连接OC,如图1,要证CE是⊙O的切线,只需证到∠OCE=90°即可;
(2)作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,易证四边形AOCF是菱形,根据对称性可得DF=DO.过点D作DH⊥OC于H,易得DH=1/2DC,从而有1/2CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即1/2CD+OD)最小,然后在Rt△OHF中运用三角函数即可解决问题.
【解答】(1)证明:连接OC,如图1所示:
∵CA=CE,∠CAE=30°,∴∠E=∠CAE=∠OCA=30°,∠COE=2∠CAE=60°,
∴∠OCE=180°﹣30°﹣60°=90°,即CE⊥OC,∴CE是⊙O的切线;
(2)解:作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,如图2所示,
则∠AOF=∠COF=1/2∠AOC=1/2(180°﹣60°)=60°.
∵OA=OF=OC,∴△AOF、△COF是等边三角形,∴AF=AO=OC=FC,
∴四边形AOCF是菱形,∴根据对称性可得DF=DO.
过点D作DH⊥OC于H,
∵OA=OC,∴∠OCA=∠OAC=30°,
∴DH=DC•sin∠DCH=DC•sin30°=1/2DC,∴1/2CD+OD=DH+FD.
根据两点之间线段最短可得:
当F、D、H三点共线时,DH+FD(即1/2CD+OD)最小,
∵OF=OA=4,∴此时FH=DH+FD=OF•sin∠FOH=√3/2×4=2√3,
即1/2CD+OD的最小值为2√3.
【点评】本题主要考查了切线的判定、等腰三角形的性质、三角函数的定义、特殊角的三角函数值、等边三角形的判定与性质、菱形的判定与性质、两点之间线段最短等知识,把1/2CD+OD转化为DH+FD是解决第(2)小题的关键.

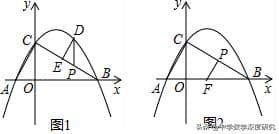
牛刀小试:1.(2018•大东区一模)如图,已知抛物线y=a/3(x+1)(x﹣3)(a为常数,且a<0)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C(0,√3),点P是线段BC上一个动点,点P横坐标为m.
(1)a的值为 _____;
(2)判断△ABC的形状,并说明理由;
(3)如图1,过点P作y轴的平行线,交抛物线于点D.
①是否存在实数m,使四边形OCDP是平行四边形?若存在,求出m的值;若不存在,请说明理由;
②过点D作DE⊥BC于点E,设△PDE的面积为S,求S的最大值.
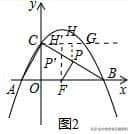
(4)如图2,F为AB中点,连接FP.一动点Q从F出发,沿线段FP以每秒1个单位的速度运动到P,再沿着线段PC以每秒2个单位的速度运动到C后停止.若点Q在整个运动过程中的时间为t秒,请直接写出t的最小值及此时点P的坐标.
【提示】(1)直接把C点坐标代入y=a/3(x+1)(x﹣3)可求出a的值为√3;
(2)利用抛物线与x轴的交点问题得到A(﹣1,0),B(3,0),则根据正切的定义和特殊角的三角函数值可求出∠ACO=30°,∠BCO=60°,则∠ACB=90°,于是可判断△ACB为直角三角形,然后根据三角形面积公式计算S△ACB;
(3)①先利用待定系数法求出直线BC的解析式为y=﹣√3/3x+√3,则可设点P的坐标为(m,﹣√3/3m+√3),D(m,﹣√3/3m²+2√3/3m+√3),易得PD=﹣√3/3(m²﹣3m),根据平行四边形的判定,当PD=OC时,四边形OCDP是平行四边形,则﹣√3/3(m²﹣3m)=√3,由于此方程没有实数解,于是可判断不存在实数m,使四边形OCDP是平行四边形;
②如图1,先利用PD∥OC得到∠EPD=∠OCB=60°,根据特殊角的三角函数值得到PE=1/2PD,DE=√3PE=√3/2PD,则S=√3/8PD²,再利用二次函数的性质得到PD的最大值为3√3/4,于是可得到S的最大值;
(4)过点C作平行于x轴的直线交抛物线于点H,如图2,作FH′⊥CH于H′,交BC于P′,利用∠PCH=30°得到PH=1/2PC,根据速度公式得到t=PH/1+PC/2,则t=PF+PH,利用两点之间线段最短可判断当F、P、H共线时,PF+PH最小,此时t=PH′=√3,然后求出F(1,0)后确定P′点的坐标即可. t的最小值为√3,此时点P的坐标为(1,2√3/3).
【点评】本题考查了二次函数的综合题:熟练掌握二次函数的图象上点的坐标特征、二次函数的性质和平行四边形的判定;会利用待定系数求函数解析式;会解直角三角形,记住特殊角的三角函数值;理解坐标与图形性质.

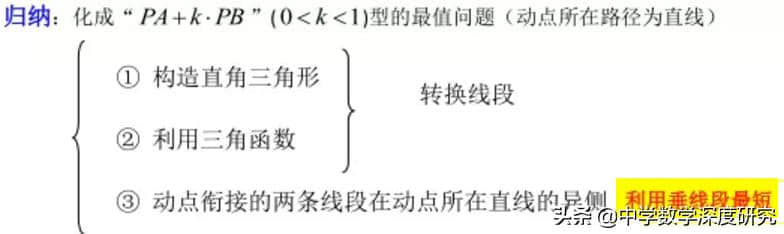
由此,我们不难得到“胡不归”问题核心解题思想就是“折转直”,胡不归问题---带系数的两线段和PA+kPB型的最值问题这一问题常规解题策略如下图总结:
真心真情真东西,讲究提供最新鲜最实用的考试素材,新学期将不断推陈出新,奉献真品,期待你的关注,相互促进。