作者不详，无门无派，这本古书被称为数学中的“独孤九剑”

如果问金庸小说中哪套剑法最厉害，很多武侠迷都会想到“独孤九剑”。剑魔独孤求败，终其一生欲求一败而不得。

其实，在数学江湖中也有一套“独孤九剑”，那便是被称为“中国数学圣经”的《九章算术》。

《九章算术》作者不详，师承不明，无门无派，身世神秘，仿佛天外飞仙般突然降临江湖，一出现便惊艳众生，引历代名家尽折腰，甘愿殚精竭虑为之作注，九章之学，遂成大宗。

刘徽（225～295），山东邹平县人，魏晋时伟大数学家，中国古典数学理论的奠基人之一，著有《九章算术注》和《海岛算经》。

正如“独孤九剑”有九式一样，《九章算术》也有九章，每章研习一术，分别是方田术、粟米术、衰分术、少广术、商功术、均输术、盈不足术、方程术、勾股术，合称“九术”，即九种算法，虽然怎么听都像是武功秘诀。

不过，你别看这些算法听上去玄乎其玄，但中国人向来务实，因此《九章算术》所研习的东西，都与老百姓的日常生活息息相关。

刘徽《九章算术注》

正所谓剑有剑招，算有算题，既然“独孤九剑”得从一招一招练起，那《九章算术》也得从一题一题做起。

整部《九章算术》说到底就是一本算题集，一共列举了二百四十六道算题，每题皆有问有答有解。这又好比二人对剑，一人出招，一人接招，至于如何见招拆招，则全赖“九术”之妙用。

九章算术篇幅巨大，其中不乏晦涩难懂的术语，咱们不妨就从中抽取比较有趣的几个章节来讲一讲，也算是抛砖引玉。

例一

箕田求积

"今有箕田，舌广二十步，踵广五步，正从三十步，问为田几何？"

说白了这其实就是个面积计算问题，由于常跟“田”打交道，这“田”也就自然成为了各类图形的代称，你比方说：“方田”指矩形，“圭田”指等腰三角形，“邪田”指直角梯形，“箕田”指等腰梯形，“圆田”指圆形等等。

而且，不同的“田”也有不同的面积计算公式——

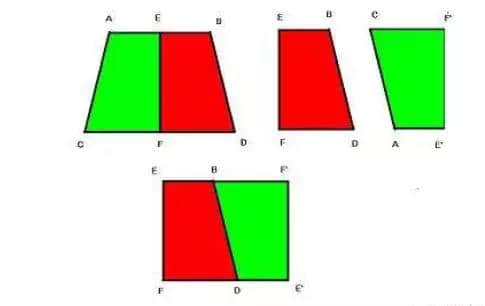
箕田术示意图

本题所求为箕田面积，也就是等腰梯形的面积，翻译过来即：

等腰梯形面积＝1/2×（上底＋下底）×高

这个公式是不是很亲切？遥想幼学当年，稚气犹未了，强记硬背，百遍后，倒也滚瓜烂熟。在此直接套用即可：

箕田面积＝1/2×（20＋5）×30＝375步

不知道古代的小学生在计算梯形面积的时候，会不会也像现在的孩子一样咬牙切齿？

例二

阳马求积

今有阳马，广五尺，袤七尺，高八尺。问积几何？

不要误会，这阳马说的可不是马，而一种特殊的锥体，本题所要求的就是这种锥体的体积。在动手计算之前，先得介绍一下立体图形家族的诸位成员。

咱们最熟悉的当然是长方体，在家族中排行最大，辈份最高，许多锥体和柱体都是由它演变而来的。

将长方体沿对角面斜分为二，得到两个一模一样的三角棱锥，称为“堑堵”，其体积是长方体的一半。

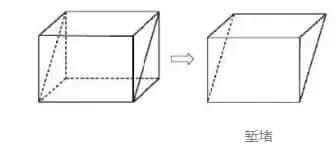
堑堵

再沿堑堵某一顶点与相对的棱剖开，得四角棱锥和三角棱锥各一个。四角棱锥以矩形为底，另有一棱与底面垂直，称为“阳马”；余下的三角棱锥是由四个直角三角形组成的四面体，称为“鳖臑”（biē nào）。

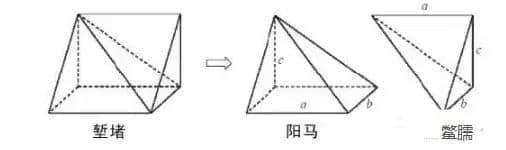
合两鳖臑而成一阳马，合三阳马而成一立方。故本题解法是：“广袤相乘，以高乘之，三而一。”

翻译一下也就是以阳马矩形底面的长乘以宽，再乘以阳马的高，得出未剖分前长方体的体积，除以三即为阳马的体积。

故答曰：“九十三尺少半尺。”

例三

凫雁相逢

今有凫起南海，七日至北海；雁起北海，九日至南海。今凫雁俱起，问何日相逢？

凫即野鸭，雁即大雁，野鸭从南海飞到北海需要七天，大雁从北海飞到南海需要九天。问：野鸭和大雁同时分别从南海和北海出发，问多少天可以相遇？

凫雁相逢

题虽然简单，却包含了均输术中的时日、路程、速度等几乎所有的元素，反映了中国古代在处理与比例分配相关的分数运算时的基本思维——“齐同”，化异分母为同分母叫“同其母”，要保持分数值不变，还必须“齐其子”，母同子齐以后才可以进行加减运算。

所以，“凫雁相逢”的解法是：“并日数为法，日数相乘为实，实如法得一日。”

也就是说，以各自需要的天数之和为除数，以各自需要的天数之积为被除数，这样就得到日数。答曰：“三日十六分日之十五。”

例四

人共买物

今有共买物，人出八，盈三；人出七，不足四。问人数、物价各几何？

题目的意思是：几个人一起买一件东西，每人出钱八块，则多三块，是为盈余；每人出钱七块，则少四块，是为不足。问人数多少？物价多少？

《九章算术》所给出的盈不足术公式相当啰嗦，反而刘徽的注更为简单——

首先计算人数。每人两次出钱，相差为8－7＝1，这是所谓“一人之差”。而“盈不足为众人之差”，也就是说由于每人两次出钱都差一点，导致了最后有3个“众人之差”，大家相差的就是盈余的3块钱和不足的4块钱之和，“众人之差”是7块钱。

“以一人之差约众人之差，故得人数也”，以7除以1，即得知人数是7人。

再来算物价。每人出8块，买1物，多3块；若买4物，则需出8×4＝32块，多3×4＝12块。每人出7块，买1物，少4块；若买3物，则需出7×3＝21块，少4×3＝12块。两次盈亏等同，互相抵消。两次出钱之和＝8×4＋7×3＝53块，共计买得4＋3＝7物。已算得人数是7人，可知物价是53块钱。

故答曰：“七人，物价五十三。”

例五

引葭赴岸

今有池方一丈，葭生其中央，出水一尺。引葭赴岸，适与岸齐。问水深、葭长各几何？

这是一道很有趣的题，说的是有一个边长为一丈的方形水池，正中央长着一根芦苇，露出水面一尺。若将芦苇稍头垂直拉到岸边，顶端恰好与岸齐平。问水有多深？芦苇有多长？

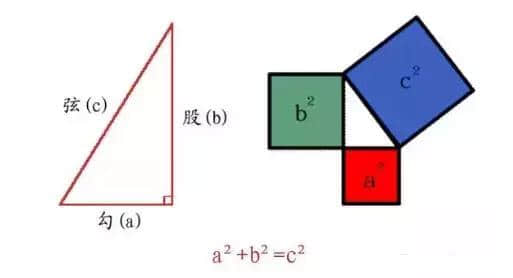
勾股定理

要解这道题，先需认识勾股定理。在《九章算术》中则称为“勾股术”，其诀曰：“勾股各自乘，并而开方除之，即弦。”换言之，即是说直角三角形两直角边的平方和等于斜边的平方。设勾为a，股为b，弦为c，则a²+b²＝c²。

据《周髀算经》记载，西周初年的数学家商高曾向周公讲过“勾三股四弦五”，即3²+4²＝5²，这是勾股定理最著名的特例。

掌握了勾股定理，要解本题就易如反掌了。《九章算术》给出的解法是：“半池方自乘，以出水一尺自乘，减之。余，倍出水除之，即得水深。加出水数，得葭长。”

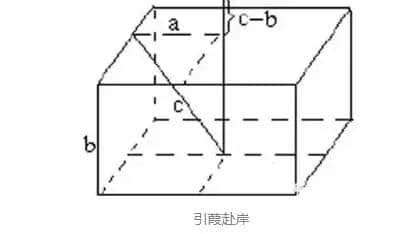
设池边长一半为a，池深为b，葭长为c

按题意，已知a＝5尺，c-b＝1尺

用勾股定理 a²+b²＝c²，可以得出

水深b＝[a²－(c－b)²]／2(c-b)＝(5²－1²)／2＝12尺

葭长c＝b＋1＝13尺

故答曰：“水深一丈二尺。葭长一丈三尺。”

“引葭赴岸”的故事宋代时还流传到了印度，被印度数学家拜斯迦罗本土化为“风吹荷花”问题：

湖静浪平六月天，荷花半尺出水面。

忽来南风吹倒莲，荷花恰在水中淹。

湖面之上不复见，入秋渔夫始发现。

落花去根三尺整，试问水深尺若干？

此题显然与“引葭赴岸”如出一辙，诗中有画，画中有题，妙趣横生。即使不做题，单纯欣赏这诗画中的意境，也会让人很开心。

至此，“九术”算是亮过了身手，但若要修炼得炉火纯青，只这般走马观花，显然是远远不够的，先得把二百四十六道题全做一遍才行！

“独孤九剑”之所以厉害，在于能克敌致胜，倘若只图花哨卖弄，遇敌时一触即溃，又怎配得上“剑魔”威名？《九章算术》亦同此理，能真真切切解决现实问题的数学，才是活泼泼有生命力的数学。

《九章算术》所归纳的种种算法，如今看来虽已不再高深，却依然被广泛应用于各个领域，非但有功于当时，亦且有裨于后世，“圣经”之誉，诚不负哉！

参考文献：

[1]闫文宇,朱宏斌.《九章算术》所反映的秦汉农业生产与社会经济[J].秦始皇帝陵博物院,2017(00):205-216.

[2]桂淑伊.管窥《九章算术》,传承数学文化[J].数学学习与研究,2017(14):124+126.

[3]王秀玉,霍艳晶.从《九章算术》中分析我国古代数学的文化风格[J].兰台世界,2014(17):151-152.

更多趣味数学历史故事，关注微信公众号：一步数学